東海中学校2026年算数第7問(解答・解説)
平行四辺形は点対称図形だから点対称の中心を通るどのような直線(例えば、対角線)によって合同な2つの図形に分けられます。
(1)も(2)もこのことを利用します。
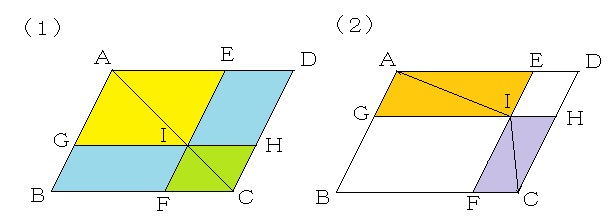
(1)
最初に述べたことから、同じ色を付けた三角形の面積は等しくなり、水色の平行四辺形の面積も等しくなります。
高さの等しい平行四辺形において、面積の比=底辺の比となるから、BF:FC=AE:ED=(9×2):12=3:2となり、平行四辺形IFCHの面積は12×2/3=8cm2となります。
三角形AIHの面積は三角形DIHの面積と等しくなります(等積変形)。
したがって、求める面積は(12+8)×1/2=10cm2となります。
(2)
最初に述べたことから、同じ色を付けた三角形の面積は等しくなるから、四角形ABCIの面積と四角形AICDの面積の差は8−2=6cm2となります。
これが三角形ACIの面積の2倍に相当する(一方は平行四辺形ABCDの面積の半分より三角形ACIの面積だけ大きく、他方は小さいからです)から、三角形ACIの面積は6/2=3cm2となります。