搶戝帥妛墍拞妛峑俀侽俀俇擭嶼悢戞係栤乮夝摎丒夝愢乯
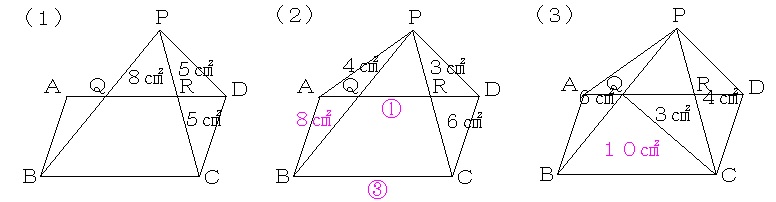
乮侾乯
崅偝偺摍偟偄嶰妏宍偺柺愊偺斾偲掙曈偺斾偼摍偟偄偐傜丄俹俼丗俼俠亖嶰妏宍俹俼俢偺柺愊丗嶰妏宍俠俢俼偺柺愊亖俆丗俆亖侾丗侾偲側傝傑偡丅
嶰妏宍俹俻俼偲嶰妏宍俹俛俠偺僺儔儈僢僪憡帡乮憡帡斾偼俹俼丗俹俠亖侾丗俀偱丄柺愊斾偼乮侾亊侾乯丗乮俀亊俀乯亖侾丗係乯偵拝栚偡傞偲丄媮傔傞柺愊偼俉亊乮係亅侾乯/侾亖俀係cm2偲側傝傑偡丅
乮俀乯
乮侾乯偲摨條偵峫偊傞偲丄俹俼丗俼俠亖俁丗俇亖侾丗俀偩偐傜丄俹俻丗俻俛亖侾丗俀偲側傝丄嶰妏宍俙俛俻偺柺愊偼係亊俀亖俉cm2偲側傝傑偡丅
傑偨丄俻俼丗俛俠亖侾丗乮侾亄俀乯亖嘆丗嘊偲側傝傑偡丅
崅偝偺摍偟偄戜宍偺柺愊斾偼乽忋掙亄壓掙乿偺斾偲堦抳偡傞偐傜丄嶰妏宍俛俠俼俻偺柺愊偼乮俉亄俇乯亊乮嘆亄嘊乯/乮嘊亅嘆乯亖俀俉cm2偲側傝丄媮傔傞柺愊偼俉亄俀俉亖俁俇cm2偲側傝傑偡丅
乮俁乯
揰俹傪捠傝曈俙俛偵暯峴側捈慄偲曈俙俢偑岎傢偭偨揰傪俽偲偡傞偲丄嶰妏宍俽俙俛偺柺愊亄嶰妏宍俽俠俢偺柺愊丄偮傑傝嶰妏宍俛俠俻偺柺愊乮暯峴巐曈宍俙俛俠俢偺柺愊偺敿暘偱偡偹乯偼俇亄係亖侾侽cm2偲側傝傑偡丅丂仼摍愊曄宍
崅偝偺摍偟偄嶰妏宍偺柺愊偺斾偲掙曈偺斾偼摍偟偄偐傜丄俻俼丗俛俠亖俁丗侾侽偲側傝傑偡丅
嶰妏宍俹俻俼偲嶰妏宍俹俛俠偺僺儔儈僢僪憡帡乮憡帡斾偼俻俼丗俛俠亖俁丗侾侽偱丄柺愊斾偼乮俁亊俁乯丗乮侾侽亊侾侽乯亖俋丗侾侽侽乯偵拝栚偡傞偲丄媮傔傞柺愊偼乮侾侽亄俁乯亊俋/乮侾侽侽亅俋乯亖俋/俈cm2偲側傝傑偡丅