渋谷教育学園幕張中学校2025年1次算数第4問(解答・解説)
(1)
大、中、小の正方形の一辺の長さを単に、それぞれ大、中、小と表記することにします。
中の正方形と大の正方形と小の正方形がくっついているところに着目すると、中2個=小1個+大1個となります。
BDは中3個、DCは大3個で、BCは、大3個+中3個となります。
Aから底辺BCに垂線(垂直な線)を引いて考えると、その垂線の長さは、
小2個+中1個+大1個
となり、この2倍(小4個+中2個+大2個)が大3個+中3個となるから、小4個=中1個+大1個となります。
最初に書いた式の4倍を考えると、
中8個=(中1個+大1個)+大4個
中7個=大5個
となるから、中:大=5:7となり、BD:DC=5:7となります。
なお、大:中:小=7:5:(7+5)/4=7:5:3となります。
(2)
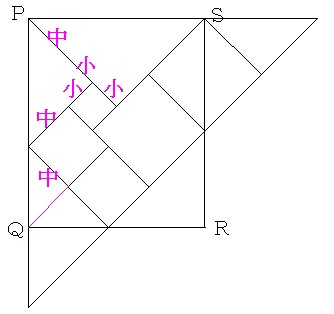
図のように、三角形ABCを長方形PQRSに重ね合わせます。
PQ:QR(PS)
=((中+小)の正方形の斜辺+中の正方形の斜辺):(中+小×2)の正方形の斜辺
=(5+3+5):(5+3×2)
=13:11
となります。