渋谷教育学園幕張中学校2024年1次算数第4問(解答・解説)
(1)
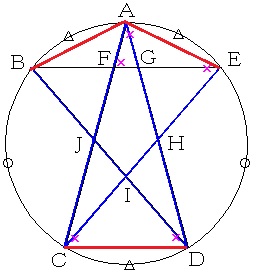
一般に、円の弧の長さ(円周上の2点を円周にそってたどったときの長さ)が等しいとき、弦の長さ(円周上の2点の最短距離)も等しくなります。
弧の長さが〇+△の弦の長さはすべて等しいから、図の青色の線の長さはすべて等しくなります。
また、弧の長さが△の弦の長さは等しいから、図の赤色の線の長さは等しくなります。
したがって、三角形ACDと三角形CEAは合同な二等辺三角形となります。
図形の線対称性(左右対称)から、BEとCDは平行となります。
平行線における同位角が等しいことと二等辺三角形の底角が等しいことを利用すると、図の×印の角の大きさがすべて等しいことがわかります。
三角形ACD(三角形CEA)と三角形EAFは相似な二等辺三角形となるから、CD=EA=EF=2cmとなります。
三角形AFGと三角形ACDは相似(相似比はAG:AD=1:4)だから、FG=2×1/4=1/2cmとなります。
(2)
三角形HCDと三角形HEGは相似(相似比はCD:EG=2:(2−1/2)=4:3)だから、HC:HE=4:3となります。
また、三角形ICDと三角形IEBは相似(相似比はCD:EB=2:(2+2−1/2)=4:7)だから、IC:IE=4:7となります。
共通部分のCEに着目して比合わせを行います。
CE=[77]とすると、IC=[77]×4/(4+7)=[28]、HC=[77]×4/(4+3)=[44]となるから、HI:IC=([44]−[28]):[28]=4:7となります。
(3)
計算が煩雑そうなので、いわゆる隣辺比(2つの三角形において、1つの角の大きさが同じまたは角の大きさの和が180度であるとき、三角形の面積比はその角をはさむ2辺の辺の比の積となる(底辺の比×高さの比と一致するからです)こと)をフル活用して解きます。
三角形AFGの面積:三角形HEGの面積
=(AG×GF):(GE:GH)
=(1×1/2):(3/2×3×3/(3+4))
=7:27
=77:297 ←あとで得られる結果の数値を確認して比合わせしています。
となります。
また、
三角形HEGの面積:三角形BIEの面積
=(GE×EH):(BE×EI)
=(3/2×([77]−[44]):(7/2×([77]−[28]))
=99:343
=297:1029
となります。
したがって、五角形FGHIJの面積は、三角形AFGの面積の
(1029−297×2)/77
=435/77倍
となります。