撿嶳拞妛峑彈巕晹俀侽俀俆擭嶼悢戞侾侽栤乮夝摎丒夝愢乯
梌偊傜傟偨嶰妏宍偺拞偵尰幚偵偼偁傝摼側偄挿偝偲妏偺慻崌偣偑偁傝傑偡偑丄偦偺偙偲偵偮偄偰偼柍帇偟偰夝偔偙偲偵偟傑偡丅
乮侾乯
嘊丄嘋丄嘍偺嶰妏宍偼丄俀曈偲偦偺娫偺妏偑偦傟偧傟摍偟偄偐傜丄崌摨偱偡丅
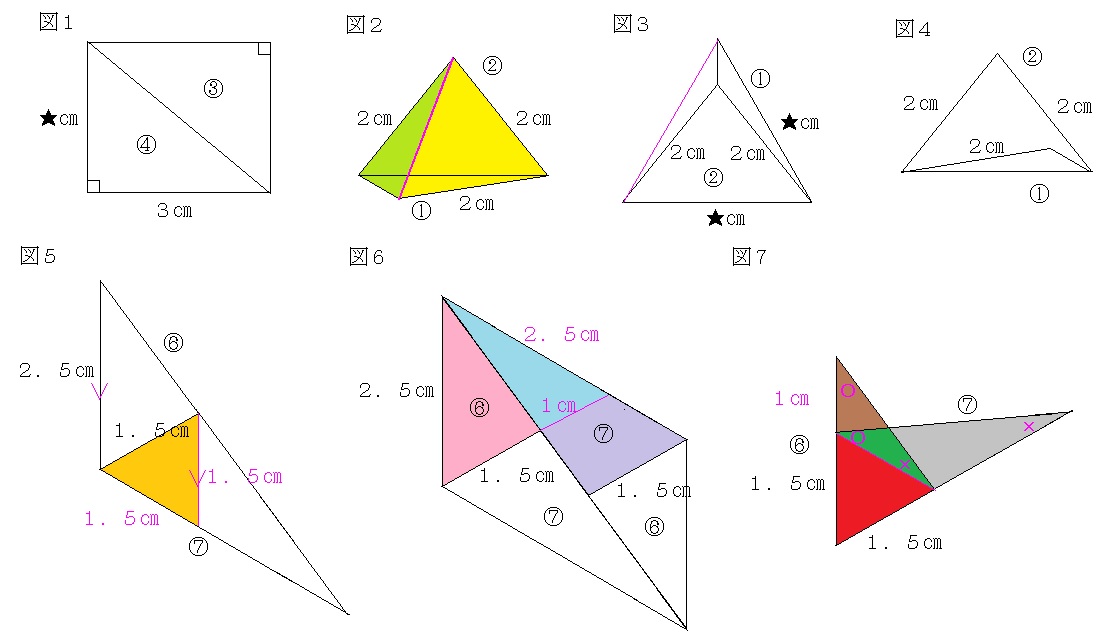
偙偺偆偪嘊偲嘋偺堦斣挿偄曈乮捈妏偺岦偐偄偺曈乮幬曈乯乯傪傄偭偨傝崌傢偣傞偲挿曽宍偵側傝傑偡乮恾侾乯丅
側偍丄嘍偺嶰妏宍偼棤曉偝側偄偲丄嘊乮嘋乯偺嶰妏宍偲慻傒崌傢偣偰傕挿曽宍傪嶌傞偙偲偑偱偒側偄偙偲偵拲堄偑昁梫偱偡丅
乮俀乯
條乆側夝朄偑峫偊傜傟傑偡丅
偙偙偱偼丄俀偮偺夝朄傪徯夘偟傑偡丅
乮夝朄侾乯
擇摍曈嶰妏宍嘇偺捀妏乮摍偟偄挿偝偺俀曈偺娫偺妏乯偼侾俉侽亅俆侽亊俀亖俉侽搙偲側傝傑偡偹丅
侾侽亄俆侽亖俇侽偵側傞偙偲偵拝栚偟偰丄嘆偲嘇偺挿偝偑仛cm偺曈傪傄偭偨傝崌傢偣傑偡乮恾俀乯丅
恾偺僺儞僋怓偺慄傪堷偔偲丄墿怓偺嶰妏宍偼丄挿偝偑俀cm偺俀曈偺娫偺妏偑侾侽亄俆侽亖俇侽搙偲側傞偐傜丄惓嶰妏宍偲側傝傑偡丅
偙偺偙偲偐傜丄墿椢怓偺嶰妏宍傕擇摍曈嶰妏宍偲側傝傑偡丅
偟偨偑偭偰丄妏傾偺戝偒偝偼
丂丂俇侽亄乷侾俉侽亅乮俉侽亅俇侽乯乸/俀
丂亖侾係侽搙
偲側傝傑偡丅
乮夝朄俀乯
擇摍曈嶰妏宍嘇偺捀妏偼俉侽搙偲側傝傑偡偹丅
侾侽亄俆侽亖俇侽偵側傞偙偲偵拝栚偟偰丄嘆偲嘇偺挿偝偑俀cm偺曈傪傄偭偨傝崌傢偣傑偡乮恾俁乯丅
恾偺僺儞僋怓偺慄傪堷偔偲丄恾宍慡懱偺嶰妏宍偼丄挿偝偑仛cm偺俀曈偺娫偺妏偑侾侽亄俆侽亖俇侽搙偲側傞偐傜丄惓嶰妏宍偲側傝傑偡丅
嵍忋偺彫偝側嶰妏宍偲嶰妏宍嘆偼丄俀曈偲偦偺娫偺妏偑偦傟偧傟摍偟偔側傞偐傜丄崌摨偲側傝傑偡丅
偟偨偑偭偰丄妏傾偺戝偒偝偼
丂丂乮俁俇侽亅俉侽乯/俀
丂亖侾係侽搙
偲側傝傑偡丅
側偍丄恾係偺傛偆側偙偲傪偟偰偼偄偗傑偣傫丅
擄偟偔側傞偩偗偱偡偐傜偹乮幚嵺丄嶼悢僆儕儞僺僢僋偱摨偠傛偆側峔恾偺栤戣偑弌偝傟偰偄傑偡乯丅
乮俁乯
條乆側夝朄偑峫偊傜傟傑偡丅
偙偙偱偼丄俀偮偺夝朄傪徯夘偟傑偡丅
乮夝朄侾乯
嘑偺巆傝侾偮偺妏偺戝偒偝偼侾俉侽亅乮俇侽亄俀係乯亖俋俇搙偲側傝丄嘐偺巆傝侾偮偺妏偺戝偒偝偼侾俉侽亅乮俇侽亄俁俇乯亖俉係搙偲側傝傑偡丅
俋俇亄俉係亖侾俉侽偵側傞偙偲偵拝栚偟偰丄嘑偲嘐偺挿偝偑侾丏俆cm偺俀曈傪傄偭偨傝崌傢偣偰丄嶰妏宍傪嶌傝傑偡乮恾俆乯丅
俇侽搙偵拝栚偟偰僆儗儞僕怓偺惓嶰妏宍傪嶌傞偲丄嶖妏偑摍偟偄偐傜丄恾偺摨偠婰崋傪晅偗偨捈慄偼暯峴偲側傝傑偡丅
恾宍慡懱偺僺儔儈僢僪憡帡乮憡帡斾偼侾丏俆丗俀丏俆亖俁丗俆乯偵拝栚偡傞偲丄僀偵偰偼傑傞悢偼
丂丂侾丏俆亊俆/乮俆亅俁乯
丂亖侾俆/係
偲側傝傑偡丅
乮夝朄俀乯
嘑偺巆傝侾偮偺妏偺戝偒偝偼侾俉侽亅乮俇侽亄俀係乯亖俋俇搙偲側傝丄嘐偺巆傝侾偮偺妏偺戝偒偝偼侾俉侽亅乮俇侽亄俁俇乯亖俉係搙偲側傝傑偡丅
俋俇亄俉係亖侾俉侽偵側傞偙偲偵拝栚偟偰丄嘑偲嘐偺挿偝偑侾丏俆cm偺俀曈傪崌傢偣偰丄嶰妏宍傪嶌傝傑偡丅丂仼偙偙傑偱偼乮夝朄侾乯偲摨偠偱偡丅
偝傜偵丄俁俇亄俀係亖俇侽偵側傞偙偲偵拝栚偟偰丄姰惉偟偨嶰妏宍偲偙偺嶰妏宍傪侾俉侽搙夞揮偝偣偨嶰妏宍傪慻傒崌傢偣偰暯峴巐曈宍傪嶌傝傑偡乮恾俇乯丅
恾偺僺儞僋怓偺慄乮墑挿偟偨慄乯傪堷偔偲丄僺儞僋怓偺嶰妏宍偲悈怓偺嶰妏宍傪崌傢偣偨嶰妏宍偼惓嶰妏宍偲側傝傑偡丅
悈怓偺嶰妏宍偲巼怓偺戜宍乮摨埵妏偑摍偟偔側傞偐傜丄暯峴側曈偑偁傝傑偡偹乯偺晹暘偺僺儔儈僢僪憡帡乮憡帡斾偼侾丗侾丏俆亖俀丗俁乯偵拝栚偡傞偲丄僀偵偰偼傑傞悢偼
丂丂俀丏俆亊俁/俀
丂亖侾俆/係
偲側傝傑偡丅
側偍丄俀庬椶偺嶰妏宍傪侾屄偢偮慻傒崌傢偣偰丄偦傟埲奜偼巊偭偰偼偄偗側偄偲柧婰偝傟偰偄側偄偺偱丄忋偺傛偆偵偟偰傕栤戣側偄偱偟傚偆丅
傑偨丄恾俇偺怓傪晅偗偨晹暘偩偗傪嶌恾偟偰夝偔乮偙偺応崌丄堦曈偺堦晹傪崌傢偣傞偙偲偵側傝傑偡偑丄堦曈傪崌傢偣傞偲偄偆忦審傪堦墳枮偨偟偰偄傞偐側偲巚偄傑偡乯偙偲傕偱偒傑偡偑丄偒傟偄偝傪廳帇偟偰忋偺傛偆偵偟傑偟偨丅
乮夝朄俁乯
摍偟偄妏搙乮俇侽搙偺偲偙傠乯傪廳偹崌傢偣偰夝偒傑偡乮恾俈乯丅
俀曈偺堦晹傪偦傟偧傟崌傢偣傞偙偲偵側傝傑偡偑丄堦曈傪崌傢偣傞偲偄偆忦審傪堦墳枮偨偟偰偄傞偐側偲巚偄傑偡丅
恾偺僺儞僋怓偺慄傪堷偔偲丄愒怓偺嶰妏宍偼丄挿偝偑侾丏俆cm偺俀曈偺娫偺妏偑俇侽搙偩
偐傜丄惓嶰妏宍偲側傝傑偡丅
偙偺偙偲偲梌偊傜傟偨忦審傪棙梡偡傞偲丄恾偺亊偺妏搙偼俀係搙丄乑偺妏搙偼俁俇搙偲側傝傑偡丅
拑怓偲椢怓傪崌傢偣偨嶰妏宍偲椢怓偲奃怓傪崌傢偣偨嶰妏宍偼丄俀慻偺妏偑偦傟偧傟摍偟偄偐傜丄憡帡乮憡帡斾偼侾丗侾丏俆亖俀丗俁乯偲側傝傑偡丅
偟偨偑偭偰丄僀偵偰偼傑傞悢偼
丂丂侾丏俆亄侾丏俆亊俁/俀
丂亖侾俆/係
偲側傝傑偡丅