南山中学校女子部2014年算数第11問(解答・解説)
京都大学1992年後期理系数学第2問・文系数学第3問をアレンジした問題です。
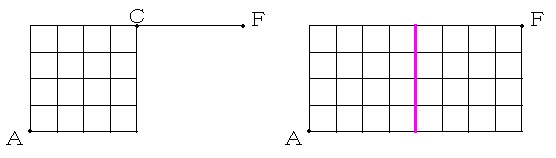
平面の図(必要な範囲における展開図)で考えます。
(1)
Cまで行くとFまでの行き方は自動的に定まるから、AからCまでの行き方を考えればいいですね。
AからCまで行くのに右に4回、上に4回(合計8回)移動することになります。
8回のうちどの4回上に行くかを考えればよく、この場合は
(8×7×6×5)/(4×3×2×1) ←組合せですね。
=70通り
あります。
(2)
AからFまで最短距離で行くためには、辺BCと辺CDの少なくとも一方(図のピンク色の線)を通ることになります。
まず、Aから辺BCを通ってFに行く場合について考えます。
AからFまで行くのに右に8回、上に4回(合計12回)移動することになります。
12回のうちどの4回上に行くかを考えればよく、この場合は
(12×11×10×9)/(4×3×2×1) ←組合せですね。
=495通り
あります。
Aから辺CDを通ってFに行く場合も同様に495通りあります。 ←条件の対等性を利用して作業を減らす!
上記2つの場合には、辺BCと辺CDをともに通る場合、つまり点Cを通る場合((1)の場合ですね)がダブルカウントされているので、取り除く必要があります。
したがって、条件を満たす場合は
495×2−70
=920通り
あります。