灘中学校2026年算数1日目第7問(解答・解説)
様々な解法が考えられますが、ここでは、正六角形の線対称の軸を引いて相似を作出し、いわゆる隣辺比に持ち込んで解く解法を紹介します。
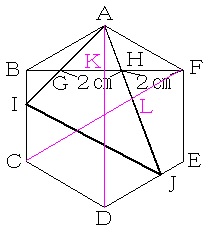
2本の対角線ADとCFを引き、ADとBF、CFとAJが交わった点をそれぞれK、Lとします。
2点K、LはそれぞれBF、AJの真ん中の点となります。
まず、三角形BIGと三角形AKGのちょうちょ相似(相似比は、BG:GK=1:(5/2−1)=2:3)に着目すると、AG:GI=3:2となり、AG:AI=3:5となります。
次に、三角形ABHと三角形FLH(相似比は、BH:FH=3:2)に着目すると、AH:HL=3:2となり、LがAJの真ん中の点であることから、AH:HJ=3:{(3+2)×2}=3:10となります。
三角形AIJの面積
=三角形AGHの面積×AI/AG×AJ/AH ←いわゆる隣辺比の利用
=三角形ABFの面積×GH/BF×AI/AG×AJ/AH ←「高さの等しい三角形の面積比=底辺の比」の利用
=正六角形ABCDEFの面積×1/6×2/5×5/3×10/3 ←正六角形の6分割を利用
=正六角形ABCDEFの面積×10/27
となります。