灘中学校2016年算数1日目第8問(解答・解説)
三角形FQRの面積が正六角形ABCDEFの面積の何倍かを求め、QS:SFの比で比例配分して、三角形QRSの面積が正六角形ABCDEFの面積の何倍かを求めるという方針で解きます。 ←三角形において、底辺一定⇒高さの比=面積の比となるから、三角形SQRの面積:三角形FSRの面積=QS:SFとなります。
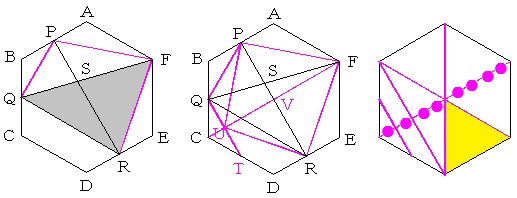
辺の比を求める場合、相似比か面積比を利用することになりますが、ここでは面積比を利用して解きます。
QS:SF=三角形PQRの面積:三角形FPRの面積となります。 ←三角形において、底辺一定⇒高さの比=面積の比となります。
次の図のように等積変形して考える(Tは辺CDの真ん中の点です)と、QS:SF=三角形PQRの面積:三角形FPRの面積=三角形PURの面積:三角形FPRの面積=UV:FVとなります。
正六角形の六分割のイメージとピラミッド相似に注目すると、UV:FV=3:4となることがわかります。
正六角形の六分割のイメージから、正六角形の1辺の長さ:正六角形の最も長い対角線(ここではCD:BE)=1:2となり、QRは、CDとBEの平均だから、正六角形の1辺の長さの(1+2)/2=3/2となります。
三角形FQRと黄色の正三角形(正六角形の1/6)は、底辺の比が
1:3/2
=2:3
で、高さの比が
2:3 ←等間隔な平行線CD、QR、BE、PW(Wは辺FEの真ん中の点)、AFを考えればすぐにわかりますね。
だから、面積比は
(2×2):(3×3) ←比の積・商〜三角形の面積比=底辺の比×高さの比
=4:9
となります。
したがって、三角形QRSの面積は、正六角形ABCDEFの面積の
1/6×9/4×3/(3+4)
=9/56倍
となります。
なお、三角形FQRの面積が正六角形ABCDEFの面積の何倍か求める際、等積変形して「方眼紙」で考えることもできます(神戸女学院中学部2003年算数第3問の解答・解説を参照)。
この問題と同様の問題が神戸女学院中学部(神戸女学院中学部2007年算数第5問)で出題されているので、そちらもぜひ解いてみましょう。
