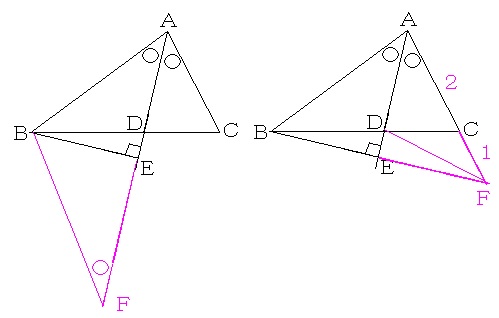
儔丒僒乕儖崅摍妛峑俀侽侾侽擭悢妛戞俀栤乮俀乯乮夝摎丒夝愢乯
條乆側夝朄偑峫偊傜傟傑偡偑丄崌摨側捈妏嶰妏宍傪俀偮慻傒崌傢偣傞偲擇摍曈嶰妏宍偑偱偒傞偙偲傪棙梡偟偨傕偺傪俀偮徯夘偟傑偡丅
乮夝朄侾乯
忋偺嵍懁偺恾偺傛偆偵丄嶰妏宍俙俛俤傪曈俛俤偵娭偟偰愜傝曉偟傑偡丅
嶰妏宍俛俥俢偲嶰妏宍俠俙俢偺偪傚偆偪傚憡帡乮憡帡斾偼俛俥丗俠俙亖俁丗俀乯偵拝栚偡傞偲丄俥俢丗俙俢亖俁丗俀亖俇丗係偲側傝傑偡丅
傑偨丄俙俤丗俤俥亖侾丗侾亖俆丗俆偲側傞偐傜丄
丂丂俙俢丗俢俤
丂亖係丗乮俆亅係乯
丂亖係丗侾
偲側傝傑偡丅
嶰妏宍俛俥俢偲嶰妏宍俠俙俢偺偪傚偆偪傚憡帡乮憡帡斾偼俁丗俀乯偵拝栚偡傞偲俛俢丗俠俢亖俁丗俀偲側傝傑偡丅丂仼妏偺擇摍暘慄掕棟傪抦偭偰偄傞恖偼俛俢丗俠俢亖俙俛丗俙俠亖俁丗俀偲偡傞偙偲傕偱偒傑偡丅側偍丄忋偺夝朄偑妏偺擇摍暘慄掕棟偺乮嬶懱揑側応崌偺乯徹柧偺侾偮偵側偭偰偄傞偙偲傕傢偐傞偱偟傚偆丅
偁偲偼丄偄傢備傞椬曈斾偺抦幆傪棙梡偡傞偩偗偱偡偹丅
丂丂嶰妏宍俙俢俠偺柺愊丗嶰妏宍俛俤俢偺柺愊
丂亖乮俢俙亊俢俠乯丗乮俢俛丗俢俤乯
丂亖乮係亊俀乯丗乮俁亊侾乯
丂亖俉丗俁
偲側傝傑偡丅
乮夝朄俀乯
忋偺塃懁偺恾偺傛偆偵丄嶰妏宍俙俛俤傪曈俙俤偵娭偟偰愜傝曉偟傑偡丅
偄傢備傞儀儞僣愗傝偺張棟偵帩偪崬傒傑偡丅
俀揰俢偲俥傪捈慄偱寢傃傑偡丅
嶰妏宍俢俛俤偲嶰妏宍俢俥俤偺柺愊傪嘊偲偟傑偡丅丂仼偙偺俀偮偺嶰妏宍偺柺愊偺崌寁傪俀攞偟偨傕偺偑俁偺攞悢偲側傞傛偆偵偙偺傛偆偵偍偒傑偟偨丅
嶰妏宍俙俛俢偺柺愊偼
丂丂嶰妏宍俛俥俢偺柺愊亊俙俠/俠俥丂仼嶰妏宍俙俛俢偲嶰妏宍俛俥俢偺嫟捠偡傞曈俛俢傪掙曈偲峫偊偨応崌丄崅偝偺斾偼俙俠偲俠俥偺斾偲堦抳偟傑偡偹丅
丂亖嘊亊俀亊俀/侾
丂亖嘖
偲側傝丄嶰妏宍俙俢俠偺柺愊偼
丂丂嶰妏宍俙俢俥偺柺愊亊俙俠/俙俥丂仼嶰妏宍俙俢俠偲嶰妏宍俙俢俥偼崅偝偑摍偟偄偐傜丄柺愊斾偼掙曈偺斾偲堦抳偟傑偡偹丅
丂亖嘖亊俀/俁
丂亖嘒
偲側傝傑偡丅
偟偨偑偭偰丄嶰妏宍俙俢俠偺柺愊丗嶰妏宍俛俤俢偺柺愊亖嘒丗嘊亖俉丗俁偲側傝傑偡丅
側偍丄俙俢丗俢俤亖嶰妏宍俙俛俢偺柺愊丗嶰妏宍俢俛俤偺柺愊亖嘖丗嘊亖係丗侾偲側傝傑偡丅