大阪星光学院高等学校2024年数学第5問(解答・解説)
(1)
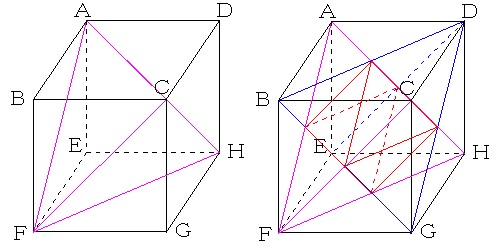
4点A、C、F、Hを結んでできる立体は(立方体にぴったり入る)正四面体になります。
三角錐F−ABCと合同な三角錐4つを立方体から取り除けばいいですね。
立方体ABCD−EFGHと比べると、三角錐F−ABCは、底面積(三角形ABC)が1/2倍、高さ(FB)が1倍で、柱体に対する錐体の体積比が1/3だから、その体積は立方体の体積の1/2×1×1/3=1/6倍となります。
結局、立体の体積は、立方体の体積の1−1/6×4=1/3倍となるから、 ←これは常に成り立つことで、知っておいた方がいいでしょう。
4×4×4×1/3
=64/3cm3
となります。
(2)
4点B、D、E、Gを結んでできる立体も4点A、C、F、Hを結んでできる立体同様、正四面体となります。
4点A、C、F、Hを結んでできる立体の各辺と4点B、D、E、Gを結んでできる立体の各辺が交わる点は立方体の各面の中心になります。
あとは、4点A、C、F、Hを結んでできる立体の同一面上の点を結ぶだけです。
2つの重なった部分の立体は(立方体にぴったり入る)正八面体になります。
この正八面体の上半分の四角すいは、立方体ABCD−EFGHと比べると、底面積(正方形)が1/2倍、高さが1/2倍で、柱体に対する錐体の体積比が1/3だから、その体積は立方体の体積の1/2×1/2×1/3=1/12倍となります。
結局、重なった部分の立体(正八面体)の体積は、立方体の体積の1/12×2=1/6倍となるから、 ←これは常に成り立つことで、知っておいた方がいいでしょう。立方体にぴったり入る正八面体と正四面体の体積比もわかりますね。
4×4×4×1/6
=32/3cm3
となります。