慶應義塾普通部2025年算数第4問(解答・解説)
①
右に5回、上に4回移動することになります。
9回の移動のうち上に移動する4回の選び方を考えればよいから、行き方は全部で
(9×8×7×6)/(4×3×2×1) ←組合せですね。
=126通り
あります。
②
最短距離で進むためには、対角線の引かれた正方形の部分では対角線を通る必要があります。 ←三角形の成立条件を考えればすぐにわかりますね。問題文にある通行止めという条件は必要ありません。この条件がなくても、道のりが最も短くなるという条件を満たすためには、CD間、EF間を通ってはいけませんからね。
対角線を最大2回通ることができることを考慮すると、通るべき経路は、下の左の図のピンク色の線になります。
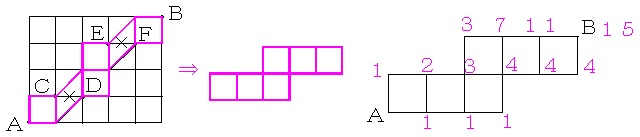
さらに、上の真ん中の図のように変形しても、行き方の総数は変わりません。 ←灘中でも同じ解法で解ける問題が出されています(灘中学校2017年算数1日目第8問)
上の右側の図のように、各交差点に最短経路の道順の数を書きこんでいくと、行き方が全部で15通りあることがすぐにわかりますね。
なお、点対称性に着目して、出迎えて落ち合うという方針を採用すると、最短経路の道順の数を半分のところまで書き込めば、3×1+3×3+1×3=15通りとすることができます。 ←この問題ではここまで考えなくても大した手間ではありませんが、灘中ではこのように考えることで大きな差が生じる問題が過去に出されています(灘中学校1995年算数1日目第3問)。
